A Heuristic Agent in Multi Agent Path Finding Under Destination Uncertainty

Lukas Berger, Marco Ragni, Bernhard Nebel

Albert Ludwig University Freiburg

Introduction

Humans are capable of recognizing intentions by solely observing another agent's actions. Hence, in a cooperative planning task, i.e., where all agents aim for all other agents to reach their respective goals, to some extend communication or a central planning instance are not necessary. In epistemic planning a recent research line investigates multi-agent planning problems (MAPF) with goal uncertainty.

Let $G = (V,E)$ be a graph. There is a set of agents $A = (a_0, a_1, ..., a_n), n \in \mathbb{N}$ located on $G$. Each agent has a specific set of possible goals $\beta : A \rightarrow 2^V$, but only one true destination $\beta^* : A \rightarrow V$. This goal is only known by the agent itself. They have a limited form of communication. Only their position, The location of the possible goals and a success statement, when reaching the true goal are communicated with each other. We will look at this problem in a round based approach.

Example of a problem instance

Example Graph

The figure shows a possible problem instance. Two different agents (blue and red robot) are located on a graph that may represent a warehouse. Both agents have a set of goals e.g. the red robot might have: $\beta(a_{red}) = \{Cables, Toys, Clothes\}$. The red robot has the true goal of $\beta^*(a_{red}) = Toys$. The blue robot on the other hand does not know the true destination of the red robot and must therefore assume, that every one of the possible goals of $a_{red}$ might be the goal it will head to.

Related Work[1]

Unlike in the usual MAPF, in MAPF/DU the execution plans are no longer linear sequences, but they they have to be branching plans. Agents branch on their real goals and make perspective shifts in order to generate plans for the other agents. A crucial concpet for understanding the structure of these branching plans are stepping stones, which are states where an agent can move towards its goal without other agents having to move, not blocking the further success of the plan. Utilizing these stepping stones, one can show that they will solve every instance, given it is solvable.

Heuristic Agent

Since the communication in MAPF/DU is sparse, an agent has to predict another agents movement, by looking at its previous actions. The possible actions an agent can make are either moving or not moving. In each round, each agent calculates its own path to its true destination. Then it checks whether or not goals of other agents can be ignored.

Ignoring goals

A goal of another agent can be ignored, if said agent does move away from the goal or it does not move for a certain amount of rounds.

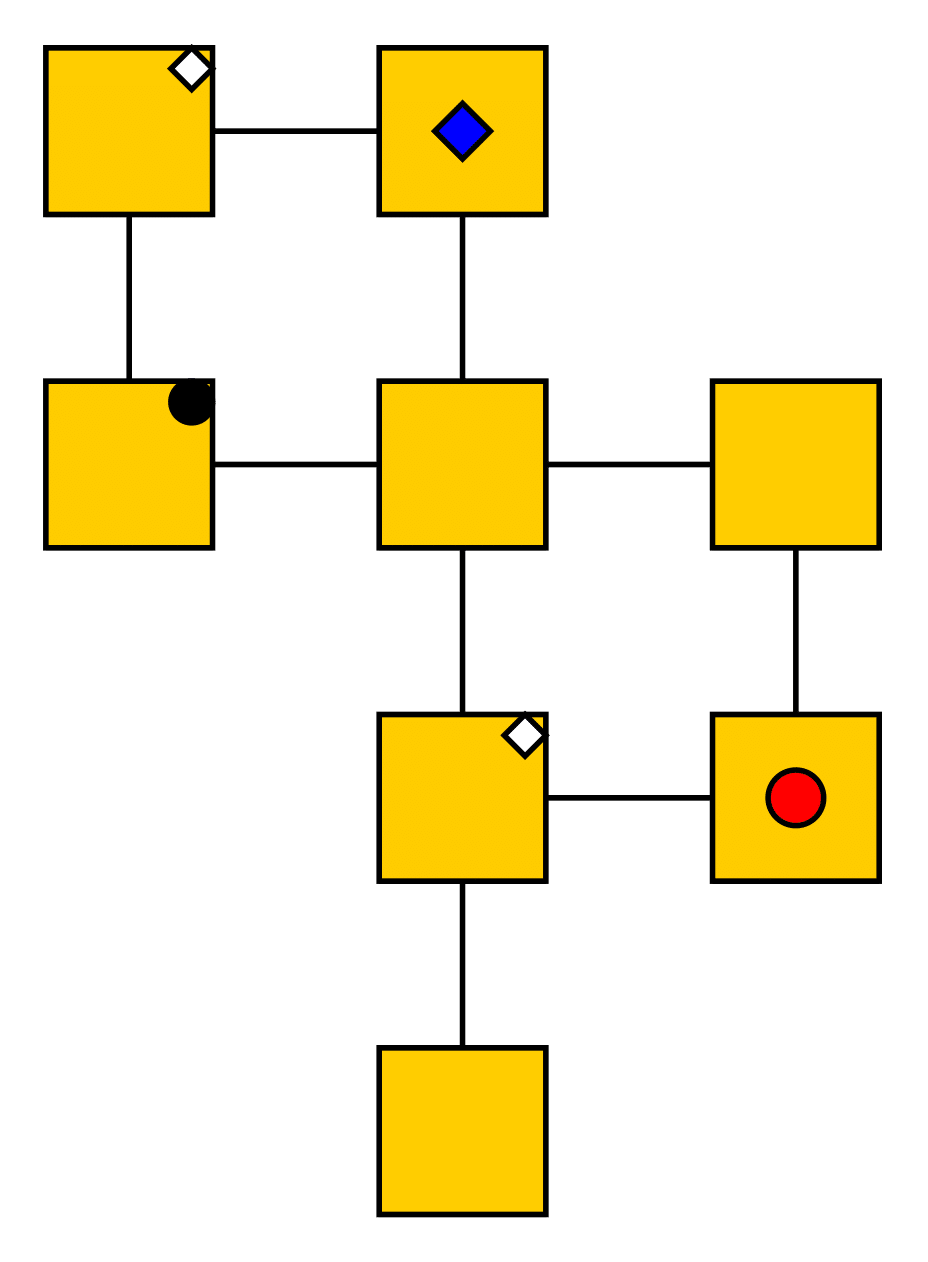first $t$
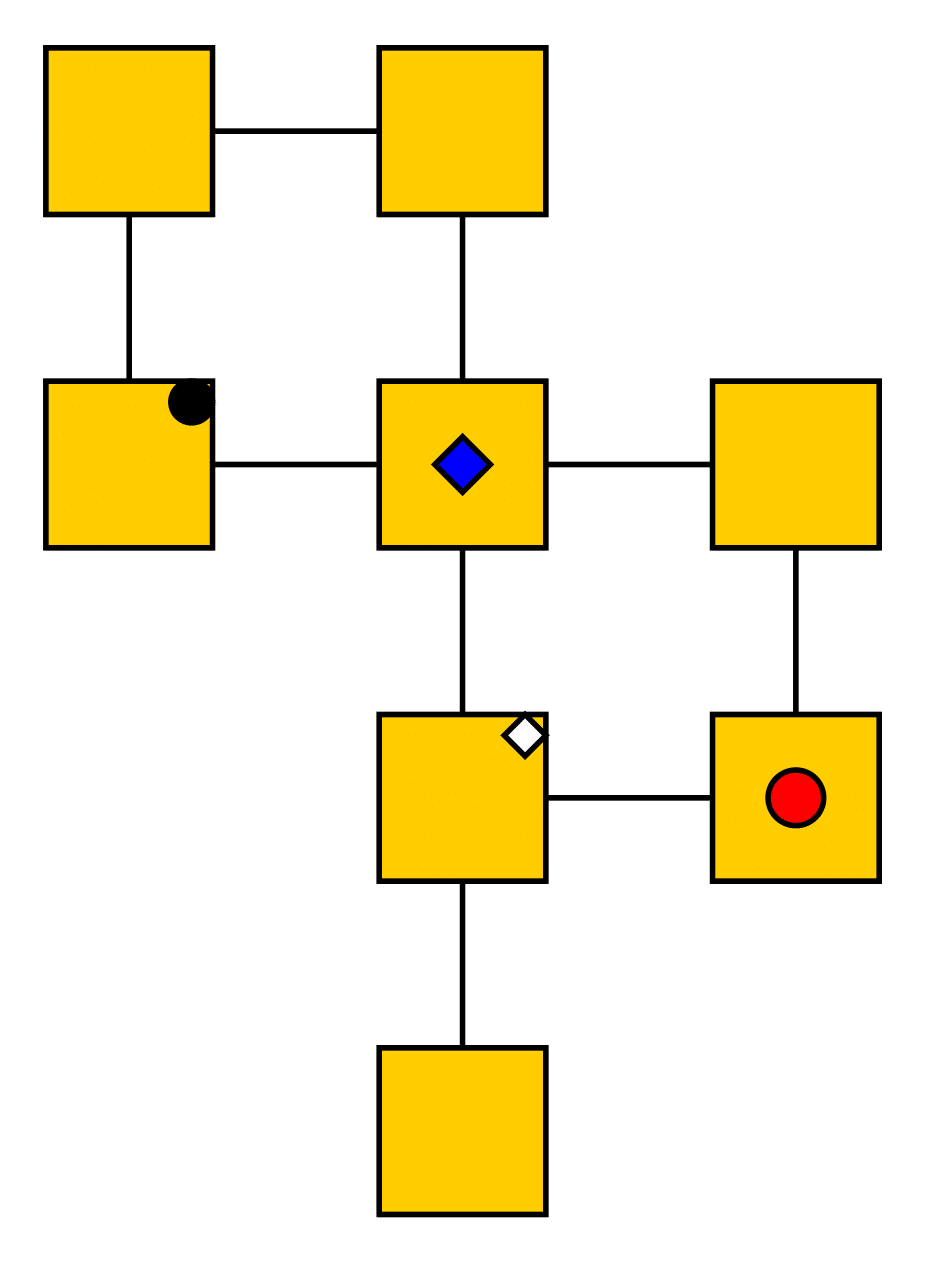second $t+1$

This is an example of the view of the red circle agent. The left figure is at some time $t$ and right at $t+1$ . The goals are the icons in the top right corner of a vertex. Black goal icons symbolize an agents true destination.

The agent then calculates all goal path of all possible goals that are not being ignored. Vertices which are not on these paths are possible escapes.

Escaping

An escape is vertex which is not on any goal path, that is not being ignored.

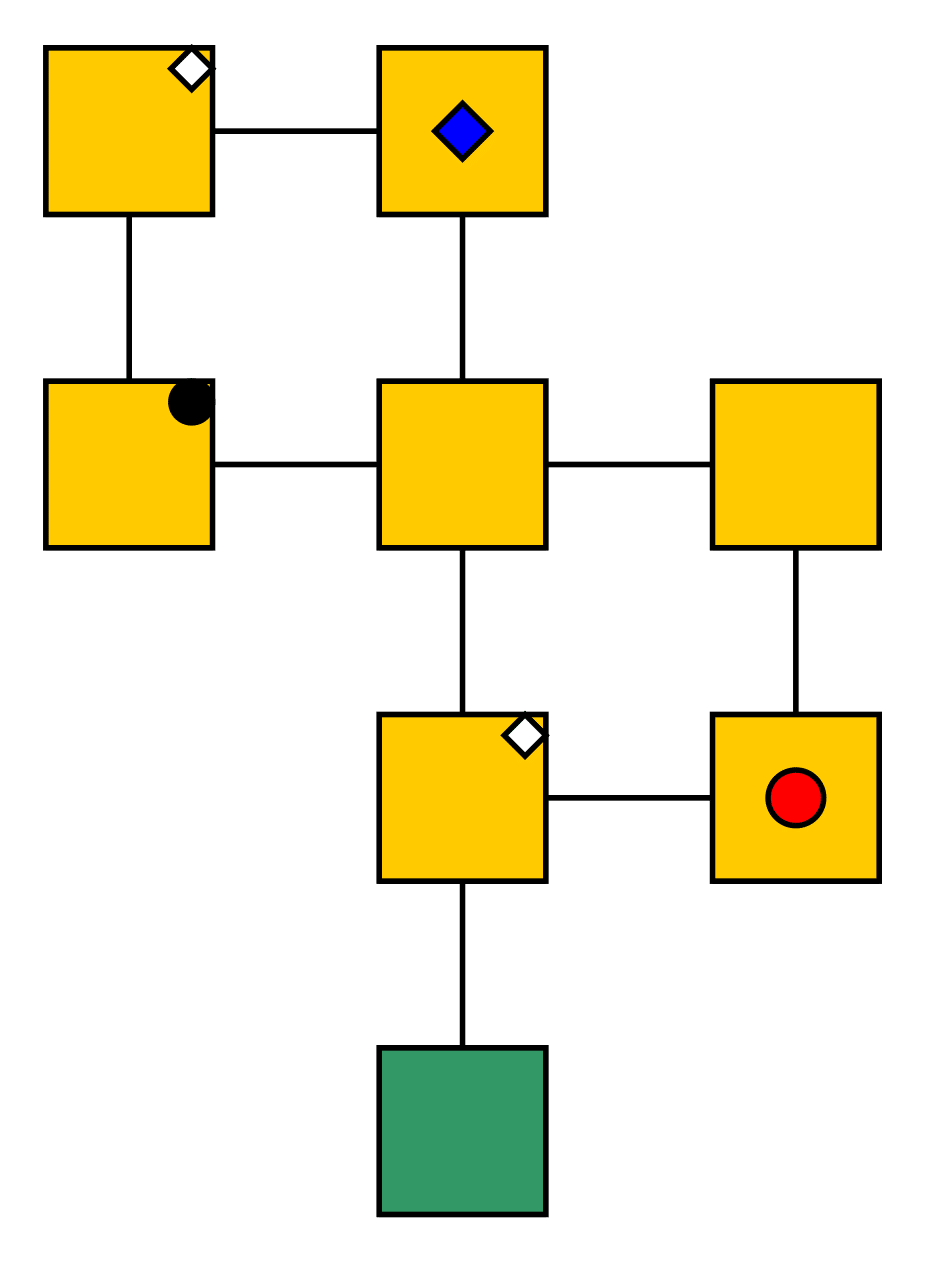first $t$
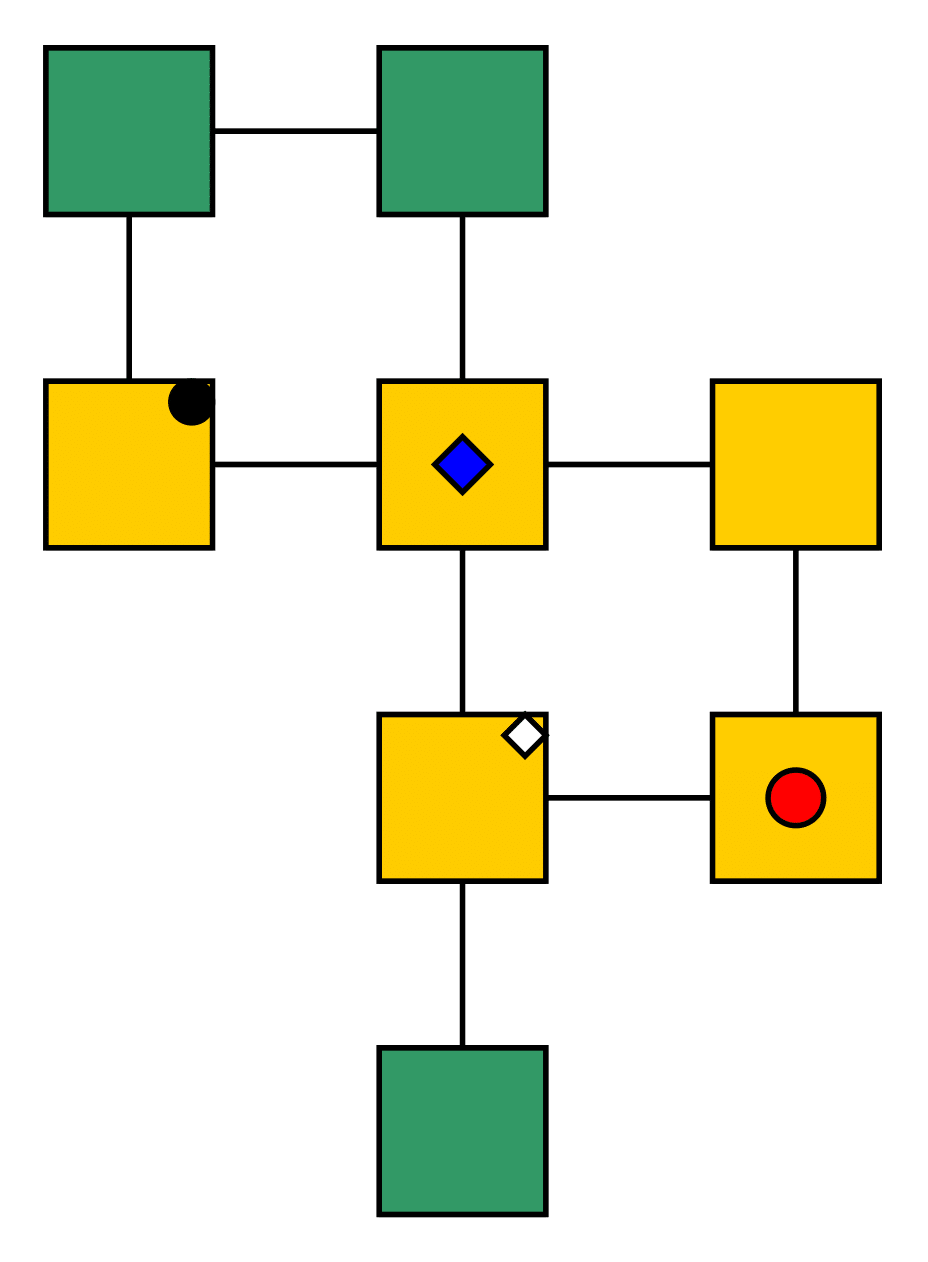second $t+1$

In this example the possible escapes for the red circle agents are marked in green. Note that these escapes can change over time, depending on an agents position and perspective.

If there are possible conflicting paths, i.e. paths of different agents that share atleast one vertex, the agent closer to an escape will move and wait until its path is clear again. If an agent reaches its true destination, it will present a success statement and finish.

Comparison of the heuristic vs coordinated implicit

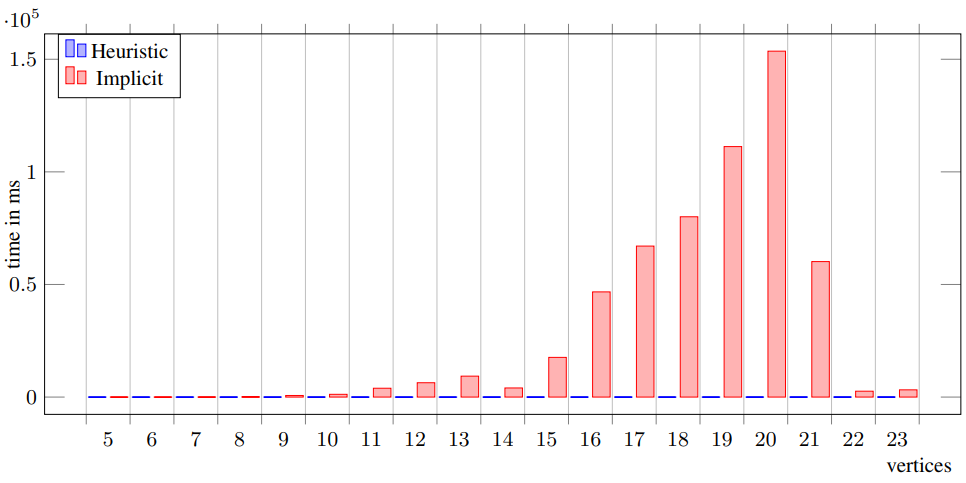
We generated[2] test instances by creating an $n \times n$, $n \in \{3, 4, 5\}$ grid-graph and randomly assigning $m \in \{2, 3 \}$ agents with $k \in \{2,3\}$ goals on the grid. Afterwards some vertices were deleted from the grid. For every combination of those values, instances were created (including duplicates), resulting in $N=35,228$ instances including unsolvable instances. Both approaches were tested on the same problem instances, measuring the time and their total solution rate (see Table). Due to runtime issues, only the heuristic agent was able to solve additional $16000$ instances with $m \in \{4,5\}$ agents, $n \in \{4,5\}$ grid size, and $k \in \{2,3\}$ goals. The graph below shows the average amount of time needed for solvable instances only. Noticeable is the large average solution time at about 13 and 20 vertices. With a higher number of agents, both approaches require a higher and higher time for solving the instances. The Table demonstrates that there is an inverse correlation between the solution rate and the number of agents.

Table

Time in ms to solve in relation to the amount of vertices of an instance

Note:

This is a heuristic planner. It is not able to solve all solvable instances. There are some configurations, where the agents are blocking each others paths. In some cases infinite execution cycles were also seen.

Conclusions and Outlook

Given the right instances, the heuristic agent is able to solve instances faster than the implicitly coordinated approach. There are some instances that cannot be solved by our approach. The implicitly coordinated planner was not designed to work in a round-based framework, it did not take into account past observations (but cf. [3]), and its main intention was to provide a method that is provably complete and correct. We are looking forward to apply similar heuristics in an asynchronous setting.

Runtime Estimation

The agent checks for every agent $a_i \in A$ if there is a conflict.Let $B$ be the set of all the goals of all agents. Because $B \subseteq V$ , there can be at most $|V|$ goals and therefore at most $|V|$ paths to the goals. The paths are calculated using the Dijkstra-Algorithm. They will not contain any cycles and are therefore at most $|V-1|$ long. All vertices are compared to the own goal path which is also at most $|V|$ long. The agent searches the graph for a suitable escape. It iterates over all vertices and all paths and compares them to each other, resulting in it being in $\mathcal{O}(|V|^3)$. It then iterates through the previously calculated escapes and determines which one is the closest (has the shortest path) to an escape for the agents. This is again in $\mathcal{O}(|V|^3)$. So every round and every agent has to solve a problem in $\mathcal{O}(|A|*|V|^3)$.

References


[1]: Nebel, B., Bolander, T., Engesser, T., Mattmuller, R.: Implicitly coordinated multi-agent path ¨ finding under destination uncertainty: Success guarantees and computational complexity. J. Artif. Intell. Res. 64, 497–527 (2019). https://doi.org/10.1613/jair.1.11376
[2]: : Implementation can be found at: https://github.com/Grintel/Cognitive-MAPFDU
[3]: Nebel, B.: Some thoughts on forward induction in multi-agent-path finding under destination uncertainty. In: Description Logic, Theory Combination, and All That - Essays Dedicated to Franz Baader on the Occasion of His 60th Birthday. pp. 431–440. Springer (2019). https://doi.org/10.1007/978-3-030-22102-7 20